Nigdy nie poznamy jej pełnej wartości. Po co nam liczba pi?

Czas czytania w minutach: 6

Pamiętam, kiedy poznałem się z główną bohaterką dzisiejszego tekstu. Lat miałem z pięć. Nudziło mi się, więc dostałem do zabawy… kalkulator. Dość prosty: poza czterema podstawowymi działaniami miał opcję wrzucenia wyniku do pamięci… I taki guzik z dziwnym kształtem: daszek na dwóch, ciut zakrzywionych, nóżkach. “Tato, a co to jest?” “To jest liczba pi”.

Tajemnicza liczba pi?

Wtedy nie byłem w stanie do końca zrozumieć, o co z tą liczbą chodzi, czemu zapisuje się ją π i dlaczego miałaby się na kalkulatorze znaleźć. Czy to 3,14 jest naprawdę takie ważne? Okazuje się, że jest. Dlaczego? Pozwól, że wyjaśnię! A wyjaśnienie zacznijmy od ustalenia, co to tak właściwie jest liczba pi. Cóż, jeśli nie spaliście na lekcjach matematyki, to powinniście wiedzieć, że liczba pi to nic innego, jak stosunek obwodu okręgu do jego średnicy. Innymi słowy: weźcie okrąg z zaznaczoną średnicą. “Rozwińcie” okrąg – tak, żeby go wyprostować. Następnie ułóżcie ten wyprostowany okrąg obok średnicy i spróbujcie zmierzyć, ile razy średnica zmieści się w wyprostowanym okręgu. Odpowiedzią powinno być “trzy i trochę”. Ale ile to jest to “trochę”?

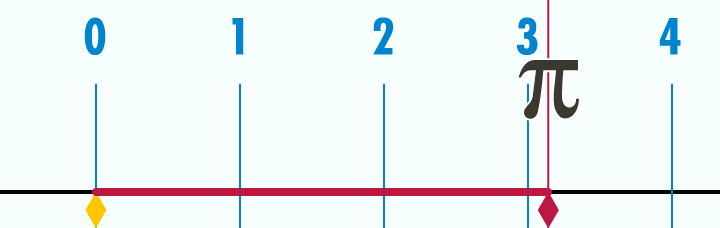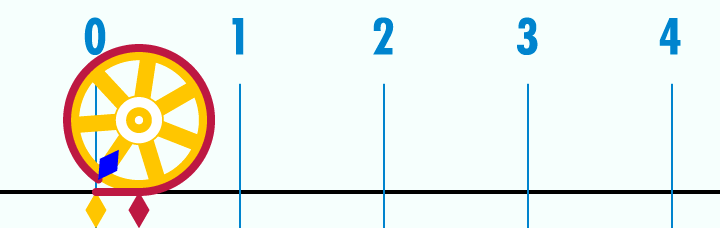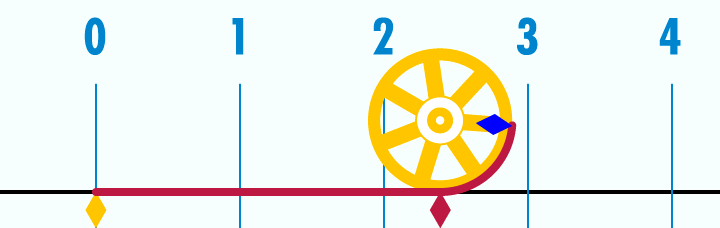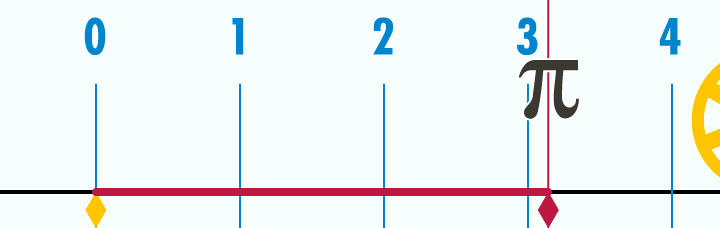
Nad tym pytaniem głowili się już starożytni. Jedno z najstarszych przybliżeń możemy znaleźć w Biblii. W Pierwszej Księdze Królewskiej, w rozdziale siódmym, opis jednego z odlewów brązowych dla świątyni jerozolimskiej głosi: “Następnie sporządził odlew „morza” o średnicy dziesięciu łokci, okrągłego, o wysokości pięciu łokci i o obwodzie trzydziestu łokci”. Sugerowałoby to przyjęcie wartości liczby pi równej trzy. Owszem, w internecie można znaleźć różne wyjaśnienia dla tego faktu, ale najprościej jest po prostu przyjąć, że w tekście zastosowano przybliżenie wykorzystywane przez Babilończyków. Na potrzeby ówczesnych budowli – wystarczało spokojnie.

Ile to w przybliżeniu?

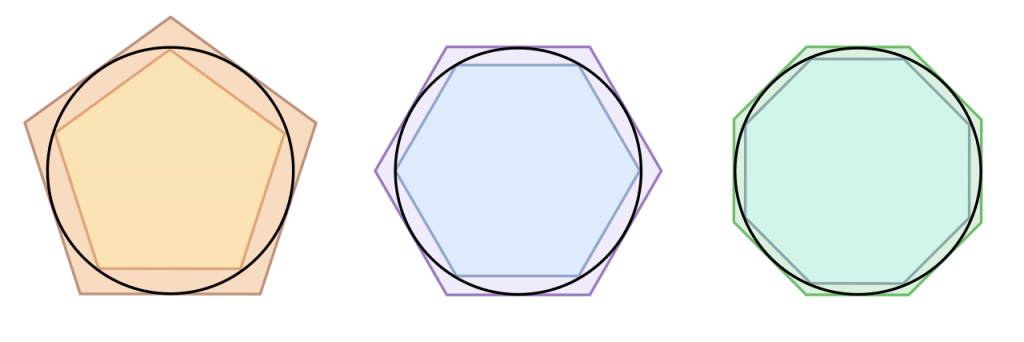
Inne przybliżenia, stosowane również w starożytnym Babilonie i Egipcie, to 22/7 albo 25/8. Zwłaszcza to pierwsze daje bardzo zbliżony do rzeczywistości wynik. Odstępstwo od faktycznej wartości to mniej niż pół procenta. Jeszcze dokładniejsze wyniki uzyskał słynny Archimedes. Udowodnił on, że liczba pi ma wartość wyższą, niż 223/71, ale mniejszą niż 22/7. Interesujące jest to, w jaki sposób to zrobił. Otóż granice liczby pi można obliczyć, wykorzystując wielokąty, zwłaszcza foremne. W jaki sposób? Koncepcyjnie – prosty. Otóż jeśli wpiszemy wielokąt foremny w okrąg, to obwód wielokąta będzie mniejszy niż obwód koła. Z drugiej strony, jeśli opiszemy taki wielokąt na okręgu, to jego obwód będzie większy niż obwód tego koła. W związku z tym dokładnie wymierzone i starannie narysowane figury mogą pomóc w ustaleniu wartości liczby pi. Na cześć greckiego uczonego i jego zasług dla określenia tej wartości liczba pi bywa też nazywana stałą Archimedesa. Można się też spotkać z nazwą ludolfina – tym razem na cześć holenderskiego matematyka, żyjącego na przełomie XVI i XVII wieku, który obliczył wartość naszej bohaterki do 35. miejsca po przecinku.

Dziś wyliczanie coraz dokładniejszych wartości nie stanowi problemu, ale też nie ma większego sensu praktycznego. Dzisiejsze komputery bez problemu wypluwają wielostronicowe rozwinięcia dziesiętne liczby pi, wyliczając miliardy bilionów miejsc po przecinku. Dla większości zastosowań nie jest to do niczego potrzebne, ponieważ zwiększona precyzja wartości liczby pi i tak “zniknie” w szumie generowanym przez niedokładne pomiary fizyczne. To po co się to w ogóle liczy? Głównie do pokazania, jaki to szybki jest nasz najnowszy i najlepszy na rynku superkomputer. Dodatkowo takie duże zbiory cyfr przydają się do badań nad losowością cyfr w rozwinięciu dziesiętnym pi.

Po co nam liczba pi?

Jednak już od przeszło dwustu lat wiemy, że “pełnej” wartości liczby pi nie poznamy nigdy. Jest ona liczbą niewymierną. Oznacza to, że nie da się jej przedstawić jako prostego ilorazu dwóch liczb całkowitych. Oznacza to również, że rozwinięcie dziesiętne liczby pi jest nie dość, że nieskończone, to jeszcze nieokresowe. Innymi słowy: nie ma w jej rozwinięciu dziesiętnym miejsca, od którego aż w nieskończoność powtarza się w kółko ten sam ciąg cyfr. W związku z tym zawsze będzie więcej cyfr do obliczenia, jeśli ktoś ma ochotę bawić się w bicie rekordów. Dodatkowo matematycy wykazali również, że pi jest liczbą przestępną. To z kolei oznacza, że nie da się jej przedstawić za pomocą skończonej liczby działań arytmetycznych i pierwiastków liczb całkowitych. To z kolei oznacza, że nie da się rozwiązać słynnego greckiego zagadnienia kwadratury koła: za pomocą cyrkla i linijki nie ma możliwości skonstruowania kwadratu o takiej samej powierzchni jak dane koło.

To wszystko jest ciekawe, ale wciąż nie wyjaśnia, dlaczego liczba pi jest tak istotna. Jej istotność dla matematyki nie powinna być zaskakująca. Jeśli chcemy obliczyć obwód koła, to robimy to z wzoru 2πr. Pole to πr². Przy sferach liczba pi zaczyna się pojawiać w trzeciej potędze. Siłą rzeczy liczba ta będzie się pojawiać również w przypadkach innych figur czy brył bazujących na okręgach i kołach. Ale nie tylko! Liczba pi bywa też bardzo przydatna na przykład do mierzenia kątów. My jesteśmy przyzwyczajeni głównie do wykorzystywania stopni, ale bardzo często wykorzystywaną jednostką są radiany. O jednostce samej w sobie kiedyś napiszemy więcej, ale warto wspomnieć, że π radianów to 180 stopni. Stąd też mniejsze kąty często są zapisywane jako ułamki pi – kąt prosty to nic innego, jak pół pi. W związku z tym nasza bohaterka często pojawi się nam tam, gdzie pracujemy z kątami. Ot, chociażby w ukochanej przez wielu uczniów trygonometrii.

Liczba pi w innych dziedzinach

Ale nawet w matematyce nie są to jedyne zastosowania liczby pi. Na przykład licząc rozkłady prawdopodobieństwa, możecie na nią natrafić. Ma jeszcze więcej, nieco bardziej egzotycznych zastosowań. Wiąże się z teorią liczb, z fraktalami i z różnymi innymi zagadnieniami… Ale wiele z nich zahacza już o fizykę! Oczywiście przede wszystkim wszędzie tam, gdzie mamy do czynienia z koniecznością policzenia czegoś związanego z kulą czy sferą możemy się spodziewać liczby pi. A trzeba pamiętać, że tych jest w Kosmosie całe mnóstwo. Jeśli cokolwiek – ot, choćby impuls światła – rozchodzi się równomiernie we wszystkich kierunkach, to w obliczeniach rozkładu energii pi może się przydać. Dlaczego? Ponieważ impuls będzie miał w każdym momencie kształt sferyczny. Również wzór na okres wahadła, które przecież poruszając się, kreśli łuki w przestrzeni, zawiera tę liczbę. Podobnie, jeśli chcemy obliczyć parametry drgania struny, bez naszej bohaterki się nie obejdzie. Spotkamy ja jednak również w wielu innych działach tej nauki.

Słyszeliście kiedyś o zasadzie nieoznaczoności? Tej, która mówi, że nie da się z idealną precyzją zmierzyć położenia i pędu cząsteczki? Działa to tak, że niepewność jednego pomnożona przez niepewność drugiego nie może być mniejsza od pewnej wartości. A wartością tą jest stała Plancka… Podzielona przez 4π. Również przy transformacji Fouriera, wykorzystywanej w przetwarzaniu sygnałów, ta liczba się pojawia. Elektromagnetyzm? Dynamika płynów? Liczba pi jest wszędzie.

Nie tylko Dzień liczby Pi

To wszystko razem przyczynia się do zadziwiającej popularności liczby pi. Być może dokłada się do tego fakt, że jest to najwcześniej poznawana stała matematyczna. Inne, takie jak e, czyli liczba Eulera, albo φ¹, czyli tak zwany złoty podział odcinka, pojawiają się dużo później. Może też mieć swój wpływ na to fakt, że liczba pi jest zdecydowanie łatwiejsza do zrozumienia, niż choćby liczba e. No i w życiu przydaje się zauważalnie częściej. Jaki by jednak powód dokładnie nie był, daje się zaobserwować, że popularność liczby pi rośnie nie tylko wśród nerdów i geeków, czy ogólniej pojętych entuzjastów nauki. Przebija się powoli do głównego nurtu.

Jak? No cóż. Konkursy na zapamiętywanie jak największej liczby cyfr rozwinięcia pi mają długą tradycję. Od pewnego czasu jednak coraz popularniejsze staje się nowe święto: Dzień liczby pi. Obchodzony jest trzeciego marca, co wynika z amerykańskiego sposobu zapisywania dat, gdzie miesiąc pojawia się przed dniem – czternasty marca to więc 3/14, a więc początek zapisu naszej bohaterki. W innych krajach próbowano wprowadzić dzień przybliżenia pi, świętowany 22 lipca². Niestety, rok nie zawiera czternastu miesięcy, żeby wykorzystać standardowy zapis dziesiętny. Tak czy inaczej, z moich obserwacji wynika, że ten zwyczaj się tak bardzo nie przyjął. Dlaczego? Być może odpowiada za niego sposób świętowania, którym jest…

Jedzenie ciasta! W języku angielski liczba pi jest homofoniczna (czyli czyta się tak samo) ze słowem pie. To zaś oznacza placek z kruchego ciasta z nadzieniem. Więc najlepszym sposobem na świętowanie dnia liczby pi jest upiec, a następnie zjeść takie ciasto. A jeszcze lepiej – kilka. Nikogo chyba nie muszę tu przekonywać, że każda wymówka, żeby zjeść ciasto, jest dobra, prawda? Zwłaszcza jeśli można w tym celu spotkać się większą grupą i dzięki temu mieć większy wybór ciast do spróbowania.

I tak też ten dzień świętowałem i świętować znów zamierzam, co też i każdemu serdecznie polecam. To, że będziecie przy okazji świętować ustanowiony niedawno Międzynarodowy Dzień Matematyki – to tym lepiej! W końcu każda inicjatywa, która zmierza do popularyzacji nauki, jest cenna i warta wsparcia. A skoro można tego wsparcia udzielić ciastem – niech żyje matematyka! Niech żyje pi! Niech żyje ciasto!

Źródła

Zainteresowało Cię to, co czytasz? Chcesz wiedzieć więcej? Śledź nas na Facebooku, i – pozwól, że wyjaśnię!